Measurement-driven reconstruction of many-particle quantum processes by semidefinite programming with application to photosynthetic light harvesting

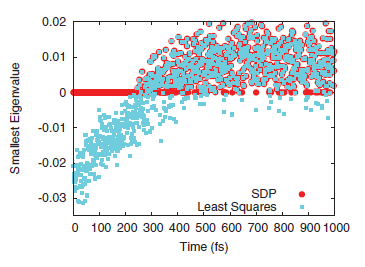
Quantum measurements provide a trove of information about a quantum system or process without solution of the Schrödnger equation, and in principle, the associated density matrix is a function of these measurements. Inversion of the measurements can produce an estimate of the density matrix, but this estimate may be unphysical, especially when the measurements are noisy or incomplete. We develop a general approach based on semidefinite programming [D. A. Mazziotti, Phys. Rev. Lett. 106, 083001 (2011)] for reconstructing the density matrix from quantum measurements which leads naturally to nonnegative solutions, a critical attribute of physically realistic solutions. We discuss the use of this methodology for reconstructing p-particle reduced density matrices (p-RDMs) of N-particle systems where additional semidefinite constraints, known as N-representability conditions, are essential because they ensure that the p-RDM represents an N-particle system. Special attention is given to the N-representability conditions for the experimentally important cases where p=1 or 2. We apply the methodology to reconstructing the time-dependent quantum process of exciton transfer in a photosynthetic light-harvesting complex.