Open-shell energies and two-electron reduced density matrices from the anti-Hermitian contracted Schrödinger equation: A spin-coupled approach

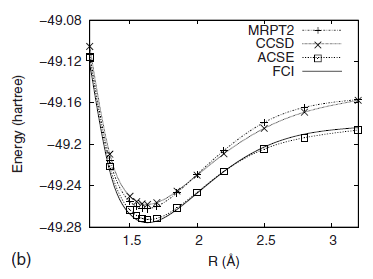
Two-electron reduced density matrices (2-RDMs) and their energies have recently been computed accurately for singlet molecular states through the solution of the anti-Hermitian part of the contracted Schrödinger equation (ACSE) [D. A. Mazziotti, Phys. Rev. Lett. 97, 143002 (2006)]. In this work we directly solve the ACSE for the 2-RDMs of open-shell molecular systems in arbitrary spin states. This generalization is achieved by spin coupling the open-shell molecule to one or more hydrogen atoms to form a singlet composite system, which can be solved by existing ACSE algorithms. Advantages of the spin-coupled approach include: (i) applicability of the singlet ACSE algorithm to high-spin open-shell molecules, (ii) consistent treatment of arbitrary spin states that avoids spin-free or other approximations to the cumulant reconstruction of higher RDMs, and (iii) computational reduction in floating-point operations and storage from exploiting the singlet spin symmetry of the composite system. The ACSE energy of the composite system we showed is the sum of the open-shell energy and the energies of the hydrogens, and the open-shell 2-RDM can be readily extracted from the composite 2-RDM. With the open-shell ACSE method we calculate energies and natural-orbital occupation numbers for a variety of doublet and triplet open-shell molecules including potential-energy curves for CH, B2, N+2, and H2O+. The ACSE produces energies that are consistently more accurate than those from either multireference second-order perturbation theory or coupled cluster singles-doubles, and as with singlet states, it provides a balanced description of single-reference and multireference correlation, which is exemplified in its dissociation of open-shell N+2. Computed 2-RDMs nearly satisfy necessary N-representability constraints.